Geodesic Dome Education:
An Introduction
by Bill Lauritzen

Geodesic dome structures, invented by R. Buckminster Fuller, have been called “the strongest, lightest, and most efficient means of enclosing space yet devised by man,” by the American Institute of Architects, but very few schools mention them. Yet the general geometric and scientific principles involved (which I have simply expressed in this article) are well within their teaching capabilities.

Principles of the Geodesic Dome
There are other more subtle factors affecting the success of the geodesic dome, but I believe there are six main factors, which I expand into 12 principles.
Teaching the Principles of the Geodesic Dome
To motivate the students you might want to suggest that you will be studying “housing for humanity,” “energy-efficient housing,” “energy-efficient buildings,” or something along these lines. With the middle school students that I worked with, I usually said we would be studying “houses of the future.” This seemed to stimulate their interest.

(1) the circle contains more area, for a given perimeter, than any other planar shape.
(2) the sphere contains more volume, for a given surface area, than any other polyhedral shape.
You may want the students to try to generalize from planar figures to spatial figures before demonstrating this principle. Using construction paper or manila folders, have the students make a very flat box (with a top), say 1 x 5 x 6 inches (in other words a surface area of 24 square inches). Now have them fill the box with beans, or saw dust, or (after lining it with plastic garbage-bag material) water. Measure the weight or volume of the box using scales (or a graduated cylinder for the water). Now make another rectangular shape with the same surface area but a different shape, say (2) x (5) x (5), and repeat the above measurement. Then try (3.0) x (4.5) x (4.5) and then (4) x (4) x (4) (cube). These shapes gradually approach a cube. The cube will hold the most substance.
I have not tried using a sphere for this experiment, but it could be done.
(3) As the surface area of a structure rises, for a given volume, the amount of construction material generally rises, other things being equal.
This should be apparent to the students. Of course, if you were comparing a dome used for an athletic event with a skyscraper, the skyscraper would require much more material because of all the interior walls.
PRINCIPLES OF THE GEODESIC DOME:
I. The economy of the sphere.
(1) the circle contains more area, for a given perimeter, than any other planar shape.
Corollary: The circle exposes less perimeter, for a given area, than any other planar shape.
(2) The sphere contains more volume, for a given surface area, than any other polyhedral shape.
Corollary: The sphere exposes less surface area, for a given volume, than any other polyhedral shape.
Corollary: For given volume and given amount of material, the sphere will form the thickest structure.
II. The conservation of materials.
(3) As the surface area of a structure rises, for a given volume, the amount of construction material generally rises, other things being equal.
(4) The cost of a structure rises as the amount of material used in construction rises, other things being equal.
III. The control of air temperature.
(5) When brought together, two substances (or masses) of different temperatures will each change their temperature toward the other’s, until they are at the same temperature.
(6) For a given mass, (such as the interior air-mass of a structure), as the amount of surface area it exposes to its surrounding environment increases, the faster it will change its temperature toward the temperature of the surrounding environment.
Corollary: For a given mass, (such as the interior air-mass of a structure), as the amount of surface area it exposes to its environment decreases, the slower it will change its temperature toward the temperature of the surrounding environment.
IV. The distribution ability of the sphere.
(7) The more distributed (spread out) a force, the easier it is to resist (or stop)
Corollary: The more concentrated a force, the harder it is to resist (or stop).
(8) For a given force, a sphere will more evenly distribute that force than any other polyhedral shape.
V. The nature of the lever.
(9) The lever can be used to move things, or hold things in place.
(10) A triangle is composed of interlocked levers which allow it to self-stabilize with a minimum of effort.
VI. The firmness of the triangle.
(11) The triangle is the only polygon that is inherently stable.
(12) When interconnected triangles are closed into a spherical shape, the resulting structure is stable.
(c) W. Lauritzen 1996


(4) The cost of a structure rises as the amount of material used in construction rises, other things being equal.
This should be apparent to the students. Of course, other factors may affect the cost, such as how many units of the structure are going to be built, the customization of the structure, mass production capabilities, etc.
(5) When brought together, two substances (or masses) of different temperatures will each change their temperature toward the other’s, until they are both at the same temperature.
This could be demonstrated easily with two beakers of water. Put one beaker at, say 40 degrees, and the other beaker at, say 60 degrees, and then allow them to mix. If they are of the same volume, then the two will mix to around 50 degrees, depending on the room temperature. (I have not tried this experiment yet so I don’t know how big a factor room temperature is.) Note that if one of the beakers is larger than the other, then it has a greater thermal energy, despite its identical temperature, and the final temperature will be closer to its temperature.
(6) For a given mass, (such as the interior air-mass of a structure), as the amount of surface area it exposes to its surrounding environment increases, the faster it will change its temperature toward the temperature of the surrounding environment.
Corollary: For a given mass, (such as the interior air-mass of a structure), as the amount of surface area it exposes to its environment decreases, the slower it will change its temperature toward the temperature of the surrounding environment.
Probably the best example of this is probably to remind students how people (and other organisms) “huddle together” when it is cold. The mass of all the people, by huddling, exposes less total skin to the outside environment. In other words, for people in the center of the huddle, more of their skin is expose to other skin, and is thereby less influenced by the cold air. You might ask the students which shape is better for huddling: a circle or a square?
(7) The more distributed (spread out) a force, the easier it is to resist (stop).
Corollary: The more concentrated a force, the harder it is to resist (stop).
One way to explain this principle is to imagine a flat book being pushed against the skin. Now imagine the exact same force on a knife being pushed against the skin. Which would you rather have pushed against you?
Another example: The sun on a normal day does not injure the skin. Now take a magnifying glass and focus that same amount of sun on a very small point on the skin. Ouch.

(8) For a given force, and given amount of material, a sphere will more evenly distribute the force than any other polyhedral shape.
This can be most easily seen by squeezing an egg with the palm of the hand. The shape of the egg distributes the force over the surface of the egg so that no one area receives the brunt of the force.
If we compare a geodesic dome to a more traditional rectangular structure (that is also triangulated) we will find that the rectangular structure has more strength in only a very small area just above the four nooks. This should be obvious as when you push directly down on a pole (one of the four corners), that pole will have great resistance to breakage compared to when you try to break it in half. The geodesic framework, like the egg, and in contrast to a rectangular structure, will spread out the force so that each strut carries only a small fraction of the total.
(9) The lever is a method of translating a force so as to move things, or hold things in place.
The mathematical principles of the lever have been well documented by Archimedes, and by most modern science textbooks, so I won’t repeat them here. Most of us are aware of how a lever is used to move something. Levers can translate a small effort across a large distance to move a large mass across a small distance (as in a crow bar). Or they can translate a large effort across a small distance to move a small mass across a large distance (as with a broom).
Levers can also be used to hold something in place, as when a wrestler uses leverage to pin his opponent to the mat. The hand brakes on a bicycle also use leverage to hold the wheel in place.
(10) A triangle is composed of interlocked levers which allow it to self-stabilize with a minimum of effort.
A scissors is a lever with the fulcrum as the pin holding the two sides together. As with all levers of this kind, to get maximum force with minimum effort one should squeeze the scissors at the outermost tips. Now if you cut off most of the length of the two blades you will have something looking more like wire cutters. Cut off the rest of the blades of the wire cutters and you will have two handles that pivot at the fulcrum. The easiest way to keep these two handles apart is two hold them (again) by their outermost tips. Slip a strut in there to keep them apart, and you have a stable triangle. Thus you can see how a triangle is composed of levers.




(11) The triangle is the only polygon that is inherently stable.
Just put the string through the straws and tie a knot. Three straws make a triangle. Some students may not know how to tie a knot. Using a thick rope about 6 feet long, I show them how to tie a square knot.
After they make a triangle, they can make a square, pentagon, hexagon, etc., until they see and feel that the triangle is the only polygon (many-side) that holds its shape.
Ask the students if they have ever noticed the triangles on bridges and towers. Some of them may have seen the triangles being used in the construction of the frame of a house or building. Because our buildings are rectangular we don’t usually notice the triangulation that is necessary for structural stability.
Bucky Fuller hypothesized that on the sub-microscopic level it is the triangulation that allows structural stability. In other words, a piece of wood can be cut into a square shape, but the unseen energy forces and patterns are in a triangular shape. Because our mathematics and science use squares and cubes to such a large extent (i.e. square centimeters, cubic centimeters, and the x-y-z axes) students may tend to miss understanding the structural importance (I should perhaps even say necessity) of the triangle. I assure you that no carpenter would.
(12) When interconnected triangles are closed into a spherical shape, the resulting structure is stable.
This principle of course brings us to the geodesic dome, which we will now discuss in some detail.
Plato’s Polyhedra
Let’s begin our creation of geodesic domes by first making some very elementary spatial shapes which are called regular polyhedra. These shapes are often referred to as the Platonic polyhedra. However, they probably were known long before him. In Euclid’s famous work, Elements, he proves, as the climax of the last “book”, Book 13, that there can be only five regular polyhedra: “I say next that no other figure, besides the said five figures, can be constructed which is contained by equilateral and equiangular figures equal to each other.” His emphasis. In other words, all of Euclid’s books seem to be leading up to this one rather simple and easy to teach fact. Yet, remarkably, we do not normally teach it.
By simply playing around with straws and string and making various shapes one can prove it to oneself rather easily. First make the five known regular polyhedra, and then see what happens when you try to find another one. I won’t spoil your fun by telling you.
Here is a breakdown of these 5 Platonic polyhedra:
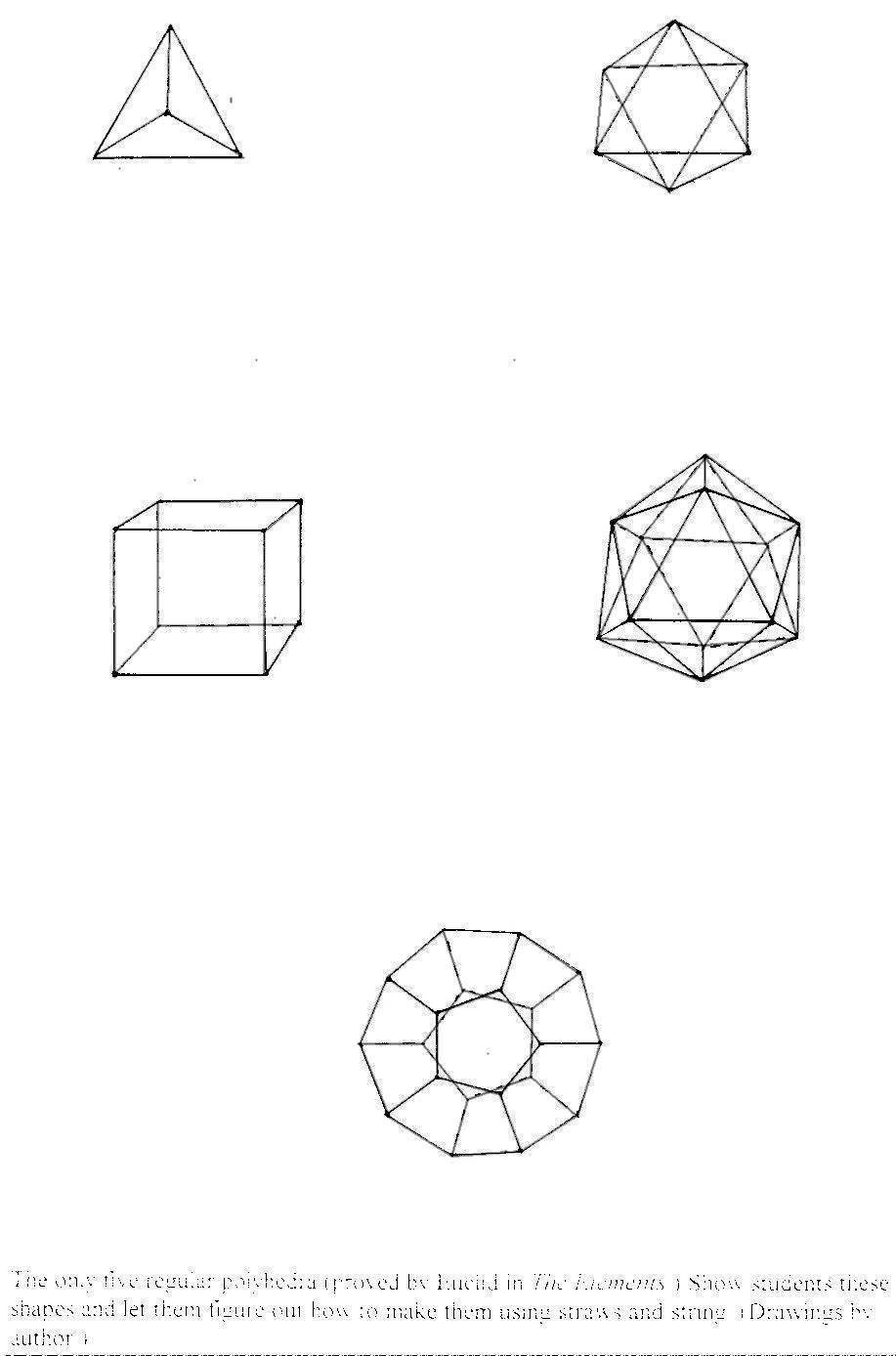
| Greek name | easy name | vertices (corners) | faces (sides) | edges |
|---|---|---|---|---|
| tetrahedron | 4-nook | 4 | 4 | 6 |
| octahedron | 6-nook | 6 | 8 | 12 |
| cube | 8-nook | 8 | 6 | 12 |
| icosahedron | 12-nook | 12 | 20 | 30 |
| dodecahedron | 20-nook | 20 | 12 | 30 |
I usually make the students memorize this chart (not the Greek names, but my names) for a quiz. (I call polygons “niks.” A dodecagon is a “12-nik.”)




The 20-Nook
I do not always have students make a 20-nook, as it, like the cube, does not hold its shape. (See principles 11 and 12.) However, if you plan on making larger geodesic domes, then have each group make one of these.
A Triangulated 20-Nook
Although the 4-nook, 6-nook, and 12-nook can be considered simple geodesic shapes, now we will consider how to make larger geodesic shapes.
Let’s take our limp 20-nook, which we just made, and make a geodesic sphere (which can later be made into a dome). If all the straws are 10 inches in length, then simply take 60 new straws and cut an inch off each of them. Now into one face of the 20-nook put five of these 9 inch straws, so that the face becomes a shallow five-sided pyramid. As you now do this to the remaining 11 faces of the 20-nook, the geodesic sphere gradually will take on a firm shape. (The Greek name for this shape is a pentikis dodecahedron which means 5-times-12-face.)
How did I know to use 9 inches? If you had simply tried using 10 inches for all the straws you would have gotten a figure with many points sticking out all around it. In this case, making certain struts shorter makes a more spherical shape.
Also, from a table I got the two numbers 0.713640 and 0.640850 for a “two-frequency icosahedral dome.” I let our 10 inch straws be similar to 0.713640. In other words, set up a proportion: 10/0.713640 = x/0.640850. If you solve for x, you get approximately 8.98, which for classroom purposes can be rounded off to 9 inches. The particular table I used, which also has pictures, is in the appendix of Polyhedra by Anthony Pugh (Dale Seymour Publications), which is still in print. The 0.713640 and 0.640850 are gotten from using 1.000000 as the radius of the sphere.

For higher level students, Pugh’s book contains information on how to calculate the lengths of straws (struts) using trigonometry.


Theory
A line is the shortest distance between two points. On a curved surface (such as a sphere) the shortest distance between two points is called a geodesic line. So a line on a flat surface, as we are used to, is a special case of a geodesic line. We might call it the flat geodesic line of a plane, versus the curved geodesic line of a sphere.
The two points on a sphere that the geodesic line connect can also be connected by a chord that cuts through the sphere. Geodesic domes use these chords as struts. We will now see how to find 1) the geodesic lines, 2) the length of these geodesic chords (struts).
By using these polyhedra, and dividing each triangulated face into further triangles, one can make very large domes. In fact, Bucky Fuller proposed covering downtown Manhattan with a dome. The surface area of the dome would be much less than the myriad, multifaceted surface area of all the enclosed buildings, making the environmental control much less costly.
Large domes are made by dividing the triangulated face into even smaller triangles. If the three sides of each triangle are “split” in two, and then these midpoints are connected, you now have four triangles inside the original triangle. If the sides of each of these four triangles are made the length of your dome’s struts, you would have what is called a “two-frequency dome.” Trisecting the sides of the original triangle, instead of bisecting, gives you a “three-frequency dome,” etc. (and 9 triangles instead of one).
If you surround your figure with a sphere so that each nook is just touching the sphere (in other words, a circumsphere), and then project all of the struts outward onto the sphere, you will have the geodesic lines of the dome. Now, as I said, the cord lengths (or strut lengths) can be calculated using trigonometry. However, in practice, many people just look in prepared tables or use a computer program. These tables give all the cord lengths for a given diameter dome.
A 2-Frequency 12-Nook
Next take the rigid 12-nook that you made earlier, and make another one, but this time for each edge put two 10 inch straws instead of one. Now make some 8 and 7/8 inch straws which will be connected to the midpoints of the edges of this large 12-nook (see figure). This 2-frequency-12-nook will need a total of 120 straws for its 120 edges. Sixty straws of 10 inches each for the 12-nook, and 60 straws of 8 and 3/4 inches each for the triangulation of the faces.
The sphere has 42 nooks and 80 faces. It has two sizes of struts: 0.546533 and 0.618034. If we let a ten-inch straw equal the 0.618034 we get the proportion:
x/0.546533 = 10/0.618034. Solving for x we get approximately 8.843. I converted the 0.843 from tenths to eighths (0.843/10 = x/8) or about 7/8 inches, giving the final length of the short straw equal to 8 and 7/8 inches.
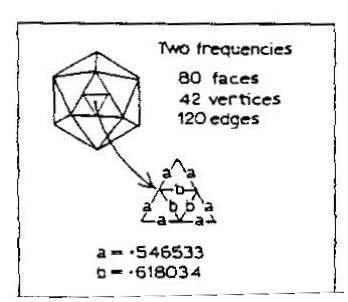
In this case, if you had used all the same length struts, you would have gotten large flat areas, triangles next to triangles in a plane, (as opposed to the “tits” of the triangulated 20-nook) and the resulting figure would have had a lot of small, stable triangles, but no overall stability because the triangles were not in a spherical pattern, as in Principle 10, in which each triangle supports other triangles.
Spheres to Domes
The 6-nook and other geodesic “spheres” that you made can be cut or “truncated”, as we did with the 12-nook, to make a dome rather than a sphere. Both of them can be cut at different places depending on how much of the sphere you want in your final dome.
Dynamic Air, Water and Earth Stability>
Notice that with the round shape of the dome, high winds of a hurricane tend to go around the dome rather than against it. During hurricanes in Hawaii and Florida, there have been occurrences of dome houses surviving, while the rectangular houses around them were destroyed. Of course, water would also tend to go around them, so large waves would be broken up. Perhaps the p and s waves from an earthquake, though moving much faster than the water or air, would also tend to go around the dome shape.


Extended Curriculum

Building the triangulated 20-nook was the climax of the 12 weeks. Before that we had started with the basics:
1) drawing lines of different lengths using a ruler.
2) drawing many angles between 0 and 360 degrees.
3) drawing a wide assortment of regular and irregular triangles, squares, pentagons, hexagons, octagons, dodecagons (12-sides), and icosagons (20-sides) using construction paper, colored pencils, protractors, and rulers.
4) measuring the sum of the angles of these figures.
5) using a compass and straight-edge to make circles and simple constructions (such as bisecting an angle, equilateral triangles, and perpendiculars).
6) making 4-nooks, 6-nooks, 8-nooks, and 12-nooks out of straws and string (as described in this article).
7) making 4-nooks, 6-nooks, 8-nooks, and 12-nooks out of construction paper.
8) reviewing and intermixing all of the above frequently.
My philosophy was to get them comfortable with these ideas and tools before moving to the more complex domes. I hope to further expand this curriculum so that there is enough material for an entire year. I believe that far too many students enter high school geometry with little or no hands-on experience with geometry, and that one year of what I call “experiential geometry” at the middle school (or high school) level would fill a great need.


Many of the students I worked with had very negative attitudes toward the police, the school, learning, and the subject matter.
My hypothesis in dealing with these students, was that the geometrical shapes, being inherently interesting, would by-pass, or short-circuit, their negative attitudes. Although I did not gather quantitative data to support this hypothesis, I was satisfied that this approach was successful due to the positive response of the students.
Reasons For Missing Dome Education
The geodesic dome was patented only in 1954 and it takes a long time for ideas to filter into textbooks, especially at the middle and elementary grades. However, why did it take someone so long to invent such an obviously (in retrospect) efficient structure? One reason is that most geometry books are essentially derived from Euclid. However, Principle 1 above, part of the economy of the sphere and thus one of the most important principles, is not contained in Euclid’s work, and is first proved, as far as I can determine, in Galileo’s book, Dialogue of the Two New Sciences (1638), where Galileo says, “the area of a circle is ... greater than that of any isoperimetric polygon.” (“Isoperimetric polygon” meaning, of course, a polygon of the same perimeter.)
Probably because Galileo’s work is about “Resistance which Solid Bodies Offer to Fracture,” and “Treating of Motion,” the geometric ideas contained in it never got transferred over to geometry books where they also belong.
Another important principle, Principle 11, concerning triangulation, is also not contained in Euclid’s (or Galileo’s) work, though, in fact, probably has been known from ancient times by artisans, mechanics, and craftsman. The lever of course is discussed by Archimedes, but is not in any geometry books. The compartmentalization of knowledge has made it a part of science.
Geometry was a one time was a hands-on science that was used to “measure the earth.” In many cases it has been stripped of any practical activity and made into purely abstract exercises. The current thrust towards cross-curricular education may help restore it to a position as a more applied science.
Because of our widespread use of squares, cubes, and other rectangular shapes in our sciences, houses, furniture, maps, city plans, etc., there is perhaps a widespread and deeply ingrained bias against non-rectangular shapes. Bucky Fuller has written extensively about this.
Summary
I successfully taught many of these principles to over 2000 middle and high school students within the Los Angeles Unified School District. In teaching these principles, I confirmed that geometry education at the middle and high school level does not have to be planar, overly bookish (as opposed to hands-on), and deal with proofs that are rarely used in the workplace. These results support the National Teachers of Mathematics Council Standards. In summary,
1) Simple principles of geodesic dome geometry can be taught to elementary, middle, and high school students, in the meaningful context of “housing for humanity” or “energy-efficient structures”, using ordinary drinking straws and string.
2) Certain factors (the economy of the sphere, the conservation of materials, the control of air temperature, the distribution ability of the sphere, the nature of the lever, and the unique firmness of the triangle) can help to explain the efficiency of the geodesic dome.
3) Certain factors (the economy of the sphere, the distribution ability of the sphere, the nature of the lever, and the unique firmness of the triangle) have been largely ignored by geometry textbooks and schools. This is probably because they are absent from Euclid’s classic work, because of the compartmentalization of knowledge, and possibly because of a cultural bias against non-rectangular shapes.
4) The negative attitude of disenfranchised inner-city youths probably can be by-passed and then changed by the use of self-stabilizing geometric models which they can build.


References:
Euclid, “Elements,” in Great Books of the Western World, Vol. 11, Encyclopedia Britannica, 1952.
Fuller, R. Buckminster, Cosmography, Macmillan, New York, 1992.
Fuller, R. Buckminster, Critical Path, St. Martin’s Press, 1981.
Galileo, “Dialogue of the Two New Sciences”, in Great Books of the Western World, Vol. 28, Encyclopedia Britannica, 1952.
Pugh, Anthony, Polyhedra, Dale Seymour Publications, Palo Alto, 1976.
Wilson, R.G., The AIA Gold Medal, McGraw-Hill, New York, 1984.
Resources:
Large Straws: (500 per box, red, about 10 inch) WinCup, 7980 West Buckley Road, Phoenix, Arizona, 85043. Small Straws: (1000 per box, red, 5.25 inch and 8 inch) Comet California Cutlery, City of Industry, CA 91748.
William Lauritzen, has been an educator for over twenty years. He holds a master’s degree in Industrial Psychology/Ergonomics.